年賀クイズの答え
今回はそれほど面倒な計算もなかったので、地道に計算すればできたかな?と思います。
Excelとかを使う場合の計算式の例もあげておきますね。
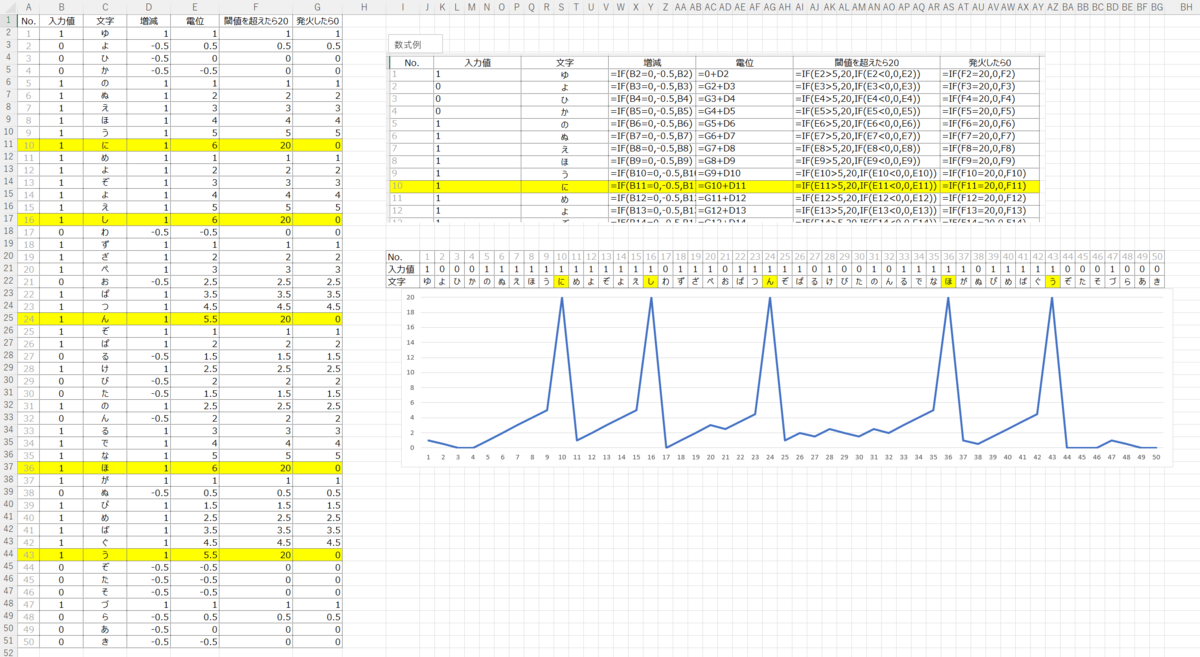
というわけで、答えは「にしんほう」、二進法でした!
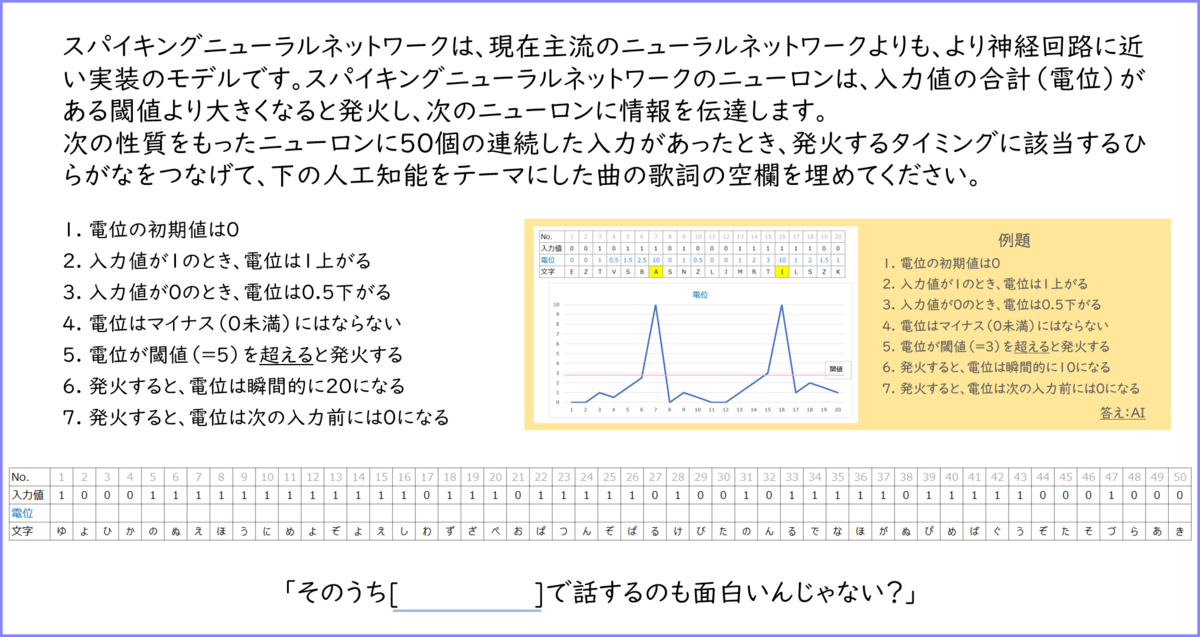
「ねぇ、そのうち二進法で話するのも面白いんじゃない?」
MOSAIC.WAVの「Mon-ju☆Brains」という人工知能を題材とした曲の一節で、
なんだかマシンのヒトに対する思いを感じられるような気がしてホロッとしちゃうんですよね。Spotifyとかでは聞くことができるので気になった方はぜひ。
open.spotify.com
MOSAIC.WAV には他にもいろいろなテクノロジーを題材とした曲(ボカロとかドローンとかVRとか量子コンピュータとかスーパーカミオカンデとかパソコンとかレコメンドシステムとか迷惑メールとかタッチパネルとかパンツとかめがねとか…)があるのでテクノロジー好きな方にはお勧めです!
というわけで、今年もよろしくお願いします。
あけましておめでとうございます
解答は 1/15(日)あたりに載せる予定です。
2022年に書いた記事など…
2022年に書いた記事をまとめておこうと思いますー。
NeuralNetwork on Scratch
Scratch で作ったニューラルネットワークです。
ミニバッチにも対応しています。
手書きの文字や図形をちゃんと学習し、認識できるようになります。
Scratch のプロジェクトは公開しているので、興味のある方は試してみてくださいね。
zenn.dev
NeuralNetwork on Scratch(アヤメの分類)
定番のアヤメの分類のやり方を書いてみました。
中身は基本的なニューラルネットワークなので、手書き文字以外でも学習できます。
zenn.dev
NeuralNetwork on Scratch(隠れ層の増やし方)
隠れ層を増やせるような実装にしてあります。
ちょっと面倒ですが…
zenn.dev
NeuralNetwork on Scratch(基本部分)
NeuralNetwork on Scratch の基本的な部分のみを取り出したものです。
余分な部分がないので、どういった構造になっているかの確認がしやすいかと思います。
(あまり需要があるとは思えませんが…)
zenn.dev
年賀クイズの答え
ということで、答えは「VOICEROID」でした!
昨年、VOICEROIDを購入したのですが、キャラクタに声がつくだけでこんなに身近に感じられるようになるのか!と結構衝撃的でした。
ということで、今回のワードは「VOICEROID」にしました。
他にもこんなことをしてたりします。
youtu.be
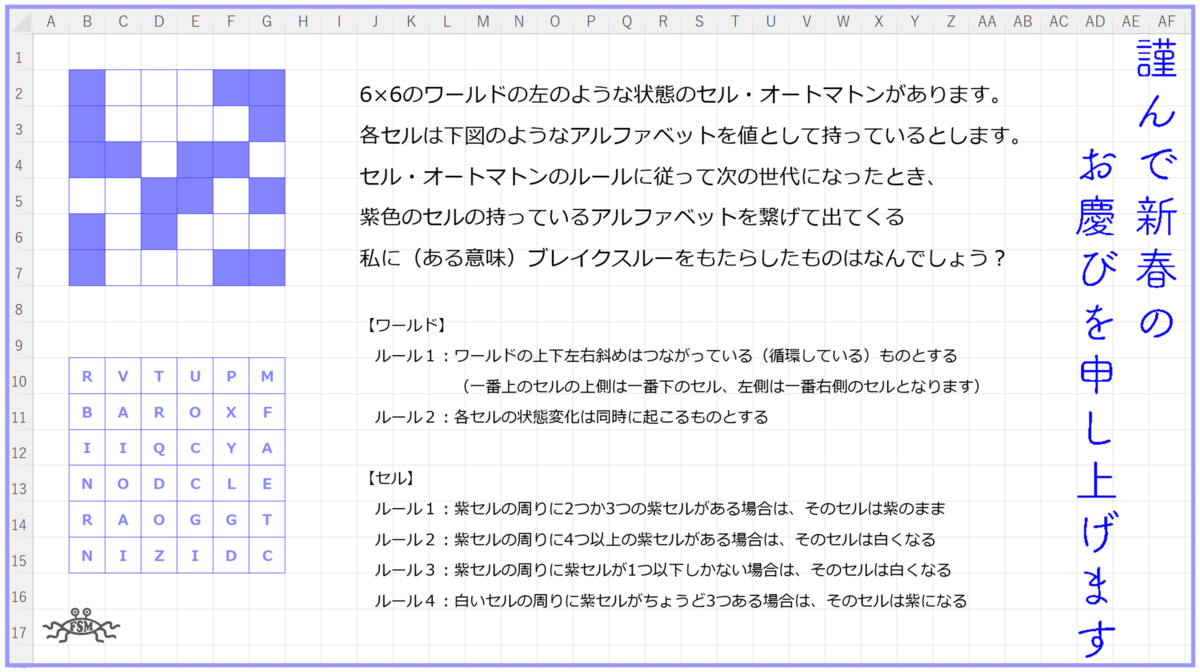
さて、セル・オートマトンの解き方ですが…年末にこんな記事を書いたので載せておきます。今回は、これを利用すれば解くことができます。
qiita.com
ですが、解答用に改変するのは面倒だと思うので、解答用のVBAコードを載せておきますね。
シートには条件付き書式設定で、セルの値が1の時には紫、0の時には白になるようにしています。
Option Explicit Public Sub Click_実行() Dim r As Long, c As Long, tc As Long Dim self As Long Dim up_r As Long, down_r As Long, left_c As Long, right_c As Long Dim life_count As Long For r = 1 To 6 For c = 1 To 6 self = Cells(r, c).Value '自分自身の状態(紫:1, 白:0) up_r = r - 1 '「上」の行番号を計算 If up_r < 1 Then up_r = 6 End If down_r = r + 1 '「下」の行番号を計算 If down_r > 6 Then down_r = 1 End If left_c = c - 1 '「左」の行番号を計算 If left_c < 1 Then left_c = 6 End If right_c = c + 1 '「右」の行番号を計算 If right_c > 6 Then right_c = 1 End If life_count = Cells(up_r, left_c).Value + Cells(up_r, c).Value + Cells(up_r, right_c).Value life_count = life_count + Cells(r, left_c).Value + Cells(r, right_c).Value life_count = life_count + _ Cells(down_r, left_c).Value + Cells(down_r, c).Value + Cells(down_r, right_c).Value If self = 1 And (life_count = 2 Or life_count = 3) Then '紫セルの周りに2つか3つの紫セルがある場合は、そのセルは紫のまま self = 1 ElseIf self = 1 And life_count >= 4 Then '紫セルの周りに4つ以上の紫セルがある場合は、そのセルは白くなる self = 0 ElseIf self = 1 And life_count <= 1 Then '紫セルの周りに紫セルが1つ以下しかない場合は、そのセルは白くなる self = 0 ElseIf self = 0 And life_count = 3 Then '白いセルの周りに紫セルがちょうど3つある場合は、そのセルは紫になる self = 1 End If Cells(r, c + 10).Value = self Next Next Application.Wait Now() + TimeValue("00:00:02") '表示遅延用Wait tc = 11 For r = 1 To 6 For c = 11 To 16 If Cells(r, c).Value = 1 Then Cells(r + 8, c).Font.Color = RGB(255, 255, 255) Cells(r + 8, c).Interior.Color = RGB(132, 132, 255) Cells(8, tc).Value = Cells(r + 8, c).Value tc = tc + 1 Application.Wait Now() + TimeValue("00:00:01") '表示遅延用Wait Else Cells(r + 8, c).Font.Color = RGB(132, 132, 255) Cells(r + 8, c).Interior.Color = xlNone End If Next Next End Sub Public Sub Click_初期化() Range("K1:P6").Value = 0 With Range("K9:P14") .Font.Color = RGB(132, 132, 255) .Interior.Color = xlNone End With Rows(8).ClearContents Range("J8").Value = "答:" End Sub
【VBA】リネームする
面白そうだったのでチャレンジしてみました。
暇なVBAerに課題置いておきます。
— ことりちゅん@えくせるちゅんちゅん (@KotorinChunChun) 2021年4月4日
a列のファイル名を、ランダムに並び替えた結果をb列に出力した後、aからbのファイル名に一括変更するマクロを書いてみてください。
さらに、変更後にミスを発見したときの為に、元のファイル名に戻すマクロも書いてください。
なかなか楽しいですよ。
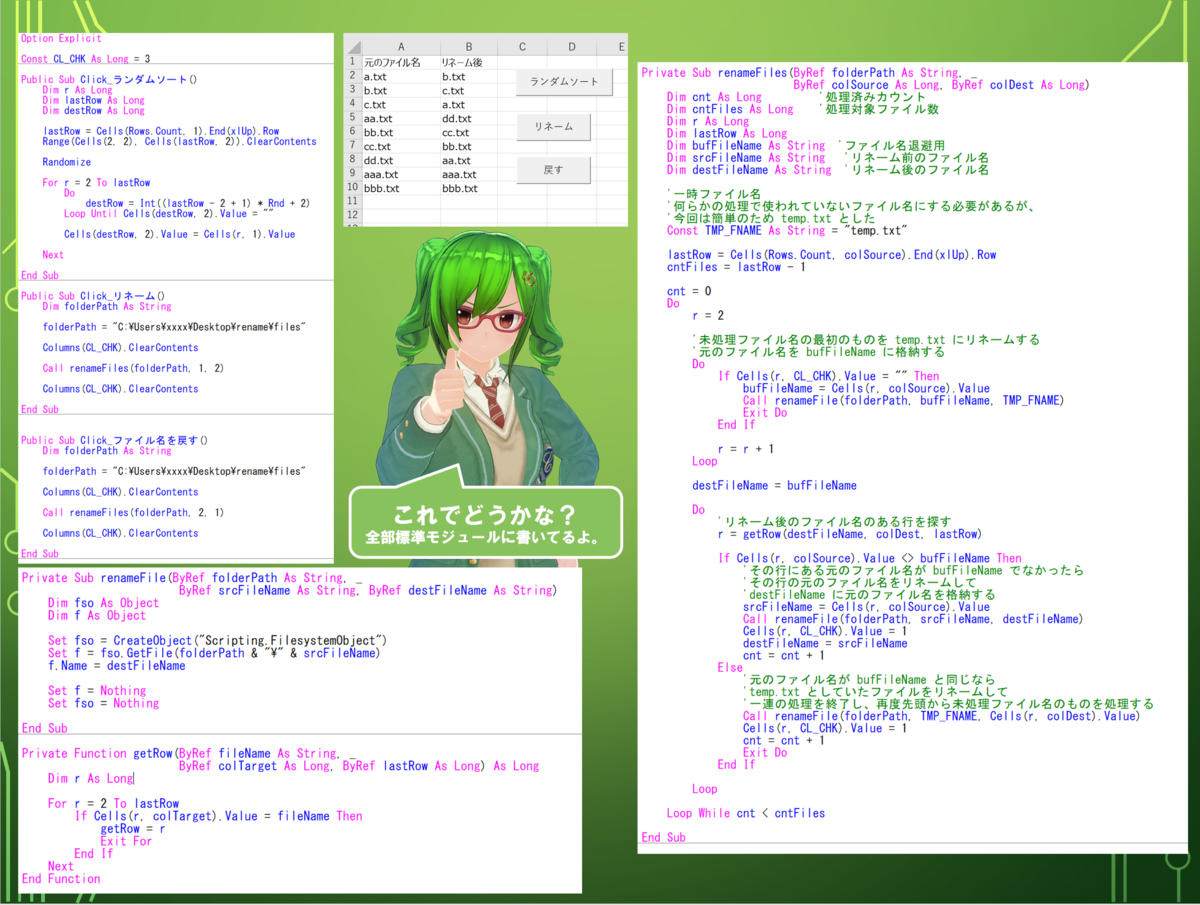
ワークシートはこんな感じ
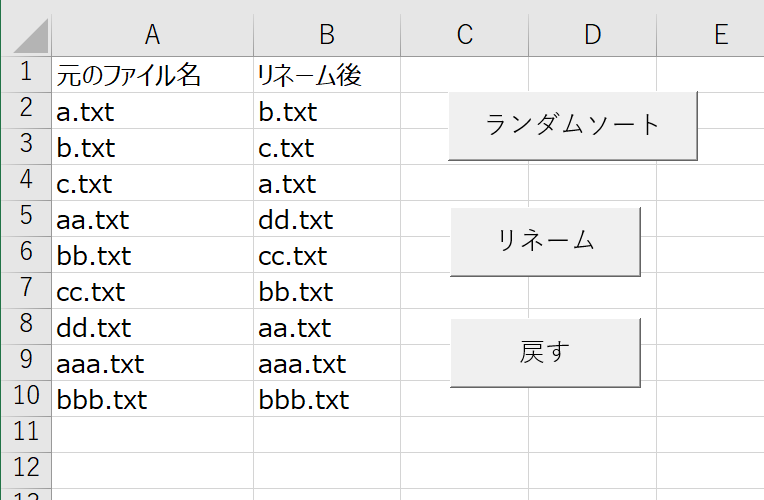
[標準モジュール] Option Explicit Const CL_CHK As Long = 3 Public Sub Click_ランダムソート() Dim r As Long Dim lastRow As Long Dim destRow As Long lastRow = Cells(Rows.Count, 1).End(xlUp).Row Range(Cells(2, 2), Cells(lastRow, 2)).ClearContents Randomize For r = 2 To lastRow Do destRow = Int((lastRow - 2 + 1) * Rnd + 2) Loop Until Cells(destRow, 2).Value = "" Cells(destRow, 2).Value = Cells(r, 1).Value Next End Sub Public Sub Click_リネーム() Dim folderPath As String folderPath = "C:\Users\xxxx\Desktop\rename\files" Columns(CL_CHK).ClearContents Call renameFiles(folderPath, 1, 2) Columns(CL_CHK).ClearContents End Sub Public Sub Click_ファイル名を戻す() Dim folderPath As String folderPath = "C:\Users\xxxx\Desktop\rename\files" Columns(CL_CHK).ClearContents Call renameFiles(folderPath, 2, 1) Columns(CL_CHK).ClearContents End Sub Private Sub renameFiles(ByRef folderPath As String, _ ByRef colSource As Long, ByRef colDest As Long) Dim cnt As Long '処理済みカウント Dim cntFiles As Long '処理対象ファイル数 Dim r As Long Dim lastRow As Long Dim bufFileName As String 'ファイル名退避用 Dim srcFileName As String 'リネーム前のファイル名 Dim destFileName As String 'リネーム後のファイル名 '一時ファイル名 '何らかの処理で使われていないファイル名にする必要があるが、 '今回は簡単のため temp.txt とした Const TMP_FNAME As String = "temp.txt" lastRow = Cells(Rows.Count, colSource).End(xlUp).Row cntFiles = lastRow - 1 cnt = 0 Do r = 2 '未処理ファイル名の最初のものを temp.txt にリネームする '元のファイル名を bufFileName に格納する Do If Cells(r, CL_CHK).Value = "" Then bufFileName = Cells(r, colSource).Value Call renameFile(folderPath, bufFileName, TMP_FNAME) Exit Do End If r = r + 1 Loop destFileName = bufFileName Do 'リネーム後のファイル名のある行を探す r = getRow(destFileName, colDest, lastRow) If Cells(r, colSource).Value <> bufFileName Then 'その行にある元のファイル名が bufFileName でなかったら 'その行の元のファイル名をリネームして 'destFileName に元のファイル名を格納する srcFileName = Cells(r, colSource).Value Call renameFile(folderPath, srcFileName, destFileName) Cells(r, CL_CHK).Value = 1 destFileName = srcFileName cnt = cnt + 1 Else '元のファイル名が bufFileName と同じなら 'temp.txt としていたファイルをリネームして '一連の処理を終了し、再度先頭から未処理ファイル名のものを処理する Call renameFile(folderPath, TMP_FNAME, Cells(r, colDest).Value) Cells(r, CL_CHK).Value = 1 cnt = cnt + 1 Exit Do End If Loop Loop While cnt < cntFiles End Sub Private Sub renameFile(ByRef folderPath As String, _ ByRef srcFileName As String, ByRef destFileName As String) Dim fso As Object Dim f As Object Set fso = CreateObject("Scripting.FilesystemObject") Set f = fso.GetFile(folderPath & "\" & srcFileName) f.Name = destFileName Set f = Nothing Set fso = Nothing End Sub Private Function getRow(ByRef fileName As String, _ ByRef colTarget As Long, ByRef lastRow As Long) As Long Dim r As Long For r = 2 To lastRow If Cells(r, colTarget).Value = fileName Then getRow = r Exit For End If Next End Function

【VBA】文字色やセル色に文字を埋め込む(抽出編)

Public Sub 文字列を抽出する() Dim txt As String Dim r As Long Dim lngRGB As Long r = 1 txt = "" Do txt = txt & decodeChar(Cells(r, 1).Font.Color) txt = txt & decodeChar(Cells(r, 1).Interior.Color) r = r + 1 Loop Until Cells(r, 1).Font.Color = rgb(0, 0, 0) MsgBox txt End Sub 'RGBの値を16進表記に変換して、赤、緑、青に分解した値を '再度10進数に変換し、それをアスキーコードとして文字に変換 Private Function decodeChar(ByVal lngRGB As Long) As String Dim res As String Dim strHex As String strHex = Right("000000" & Hex(lngRGB), 6) res = code2char(CLng("&H" & Right(strHex, 2))) res = res & code2char(CLng("&H" & Mid(strHex, 3, 2))) res = res & code2char(CLng("&H" & Left(strHex, 2))) decodeChar = res End Function Private Function code2char(ByVal ascCode As Long) As String If ascCode = 0 Or ascCode = 255 Then code2char = "" Else code2char = Chr(ascCode) End If End Function